Practical 4 - Elements of solution¶
A solution for the Lambertian and Phong local illumination models is provided. The vertex shader is the same in both cases, and the fragment shader of the Lambert model is the Phong model’s one with simply \(K_a=0\) and \(K_s=0\).
The Phong model is given by:
\(I = K_a + K_d (\mathbf{n} \cdot \mathbf{l}) + K_s (\mathbf{r} \cdot \mathbf{v})^s\),
All vectors must be oriented outwards from the fragment:
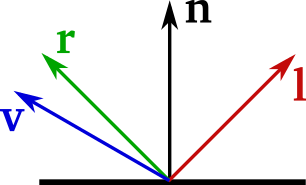
Vertex shader¶
The vertex shader phong.vert is:
#version 330 core
// input attribute variable, given per vertex
in vec3 position;
in vec3 normal;
uniform mat4 model, view, projection;
// position and normal for the fragment shader, in WORLD coordinates
out vec3 w_position, w_normal; // in world coordinates
void main() {
vec4 w_position4 = model * vec4(position, 1.0);
gl_Position = projection * view * w_position4;
// fragment position in world coordinates
w_position = w_position4.xyz / w_position4.w; // dehomogenize
// fragment normal in world coordinates
mat3 nit_matrix = transpose(inverse(mat3(model)));
w_normal = normalize(nit_matrix * normal);
}
Remember (or learn!) that normals cannot be transformed directly with the model matrix, which would yields inconsistent results for a transform with non-uniform scaling components. Instead, normals but be transformed with the NIT matrix (Normal Inverse Transform): \((M^{-1})^\top\) where \(M\) is the upper left 3x3 matrix of the mode matrix. This point has been discussed in the first lecture. More information could be found in this article.
Note
Where to compute the NIT matrix?
In our educational context, the NIT matrix is here computed in the vertex shader. However, this is very inefficient since the same computation is done for each vertex! In real life, you must compute this matrix once in the CPU side and pass it to the vertex shader as a uniform mat3.
In Python the NIT computation would be:
model3x3 = model[0:3, 0:3]
nit = np.linalg.inv(model3x3).T
Fragment shader¶
The fragment shader phong.frag is:
#version 330 core
// fragment position and normal of the fragment, in WORLD coordinates
in vec3 w_position, w_normal;
// light dir, in world coordinates
uniform vec3 light_dir;
// material properties
uniform vec3 k_d, k_a, k_s;
uniform float s;
// world camera position
uniform vec3 w_camera_position;
out vec4 out_color;
void main() {
// Compute all vectors, oriented outwards from the fragment
vec3 n = normalize(w_normal);
vec3 l = normalize(-light_dir);
vec3 r = reflect(-l, n);
vec3 v = normalize(w_camera_position - w_position);
vec3 diffuse_color = k_d * max(dot(n, l), 0);
vec3 specular_color = k_s * pow(max(dot(r, v), 0), s);
out_color = vec4(k_a, 1) + vec4(diffuse_color, 1) + vec4(specular_color, 1);
}
Note that:
All normal vectors are oriented outwards, following the Phong’s model convention.
All normal vectors must be normalized. Since
w_normalis interpolated from the vertices’ normals, its direction is correct but its norm could be different than 1.w_camera_positionis the position of the camera in the world coordinates. We will detail this point below.In the GLSL
reflect()function, the first parameter is the incident vector. With the Phong’s model orientation convention, this is then-l.Don’t forget to clamp negative scalar products to 0 (which occurs when the light is located behind the surface)
The w_camera_position variable contains the position of the camera in the world referential. It can be computed from the view matrix:
The camera position is at the origin in the view referential. Let pose \(\mathbf{c}_v=(0,0,0,1)\)
We look for the camera position \(\mathbf{c}_w\) in woorld coordinates. What we know is that \(\mathbf{c}_v = \mathbf{view} * \mathbf{c}_w\), thus \(\mathbf{c}_w = \mathbf{view}^{-1} * \mathbf{c}_v\). Since \(\mathbf{c}_v=(0,0,0,1)\), \(\mathbf{c}_w\) is just the translation part of the inversed view matrix!
If computed in the fragment shader, the same operation would be repeated numerous times. Instead, the camera position is usually computed in the CPU side and hen transfered as a uniform variable. In our framework, this is done in the
Viewer::runmethod.
Note
Complementary exercise: in the view frame?
Not you sure you understood everything? You can also compute the illumination model in view coordinates instead of in world coordinates. The v vector is straightforward to obtain since the camera’s position is at the origin. However, all lights must be transformed from the world to the view referential.
Try to compute your illumination in the view referential, and make sure the rendering is the same!
Illumination parameters¶
Common material parameters such as \(\mathbf{K}_d\), \(\mathbf{K}_s\) or \(s\) are sent to the shaders as uniforms. What values are sent?
Peek at the Viewer::load method in file core.py: a dictionnary of uniforms is created with default values for the illumination parameters. All these uniforms will be sent to the shaders.
uniforms = dict(
k_d=mat.get('COLOR_DIFFUSE', (1, 1, 1)),
k_s=mat.get('COLOR_SPECULAR', (1, 1, 1)),
k_a=mat.get('COLOR_AMBIENT', (0, 0, 0)),
s=mat.get('SHININESS', 16.),
)
When a material is used in a mesh (typically from vp.mtl), illumination values of this material override the previous values in the uniforms dictionary.
Finally, you can use your own parameters by explicitly defining them as extra parameters in the load method. These parameters will be added in the dictionary, overridding any existing entry. For example:
viewer.add(*load('suzanne.obj', shader, light_dir=light_dir, K_d=(.6, .7, .8), s=100))
Optional exercises¶
Exercises 3 to 5 won’t be corrected here. No new notion is required, you should be able to manage everything yourself.
If needed, come back to your teachers to discuss your proposed solution.